SPSS Mann-Whitney U 检验教程

作者：Ruben Geert van den Berg，分类：非参数检验 & 统计学 A-Z

简介与练习数据文件

当数据不满足独立样本 t 检验的假设时，Mann-Whitney U 检验是其替代方法。最常见的情况是在小样本（例如，n < 25）中检验非正态分布的因变量。由于中心极限定理，在较大样本中，非正态性不是一个严重的问题。

Mann-Whitney U 检验也称为独立样本的 Wilcoxon 检验，不要与相关样本的 Wilcoxon 符号秩检验混淆。

研究问题

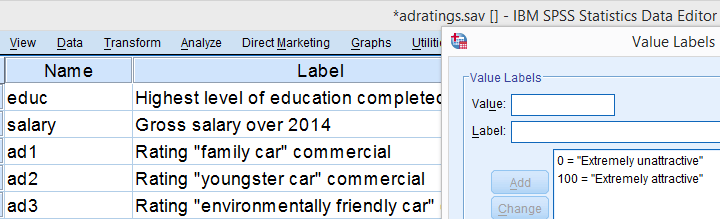
在本教程中，我们将使用 adratings.sav 数据文件，截图如上所示。这些数据包含 18 位受访者对 3 个汽车广告的评分，这些受访者在性别和年龄类别上是平衡的。我们的研究问题是男性和女性对我们的广告的评价是否相似。对于每个广告，我们的零假设是：“男性和女性的平均评分相等。”

快速数据检查 - 分割直方图

在运行任何显著性检验之前，让我们首先检查一下我们的数据是什么样的。一个很好的方法是运行一些直方图。由于我们对男性和女性受访者之间的差异感兴趣，让我们按性别分割我们的直方图。以下截图将指导你完成此操作。

SPSS Mann-Whitney U 检验 - 分割直方图菜单

分割直方图 - 语法（Syntax）

使用菜单会产生下面的第一个语法块。我们复制粘贴两次，替换变量名并运行它。

***运行分割直方图以查看数据是否合理。***
GRAPH
/HISTOGRAM=ad1
/PANEL COLVAR=gender COLOP=CROSS.

GRAPH
/HISTOGRAM=ad2
/PANEL COLVAR=gender COLOP=CROSS.

GRAPH
/HISTOGRAM=ad3
/PANEL COLVAR=gender COLOP=CROSS.

分割直方图 - 结果

最重要的是，所有结果看起来都是合理的；我们没有看到任何不寻常的值或模式。其次，我们的因变量似乎不是正态分布的，并且我们的总样本量只有 n = 18。这反对使用 t 检验来分析这些数据。最后，通过仔细观察分割直方图，你已经可以看到哪些广告更受男性受访者欢迎，哪些更受女性受访者欢迎。但是，即使大量男性和女性人群的评价完全相似，我们仍然会在小样本中看到_一些_差异。然而，如果零假设（即总体均值相等）确实为真，那么_大的_样本差异是不太可能的。我们现在将找出我们的样本差异是否足够大，可以反驳这个假设。

SPSS Mann-Whitney U 检验 - 语法（Syntax）

注意：选择 E xact 会产生额外的语法行（下面省略）。

***一次对 3 个因变量运行 Mann-Whitney 检验。***
NPAR TESTS
/M-W= ad1 ad2 ad3 BY gender(0 1)
/MISSING ANALYSIS.

SPSS Mann-Whitney U 检验 - 输出描述性统计

Mann-Whitney 检验基本上用它们的秩次替换所有分数：对于 18 个案例，分别是 1、2、3 到 18。较高的分数得到较高的秩次。如果我们的分组变量（性别）不影响我们的评分，那么男性和女性的平均秩次应该大致相等。

我们的第一个广告（“家庭用车”）显示了男性和女性受访者之间平均秩次的最大差异：女性似乎更喜欢它。对于其他两个广告，观察到相反的模式，但要弱得多。

SPSS Mann-Whitney U 检验 - 输出显著性检验

根据你的 SPSS 许可证和样本大小，下面显示的一些输出可能不存在：对于 n = 40 或更少的案例，你将始终获得一些精确的结果。

Mann-Whitney U 和 Wilcoxon W 是我们的检验统计量；它们用一个数字概括了平均秩次的差异。请注意，Wilcoxon W 对应于上表中最小的秩次总和。我们更喜欢报告 Exact Sig. (2-tailed) （精确显著性，双尾）：针对联系修正的精确 p 值。第二好的是 Exact Sig. [2*(1-tailed Sig.)] （精确显著性 [2*(单尾显著性)]），精确的 p 值，但未针对联系进行校正。对于较大的样本量，我们的检验统计量大致呈正态分布。近似的（或“渐近的 (Asymptotic)”）p 值基于标准正态分布。SPSS 报告的 z 分数和 p 值是在没有应用必要的连续性校正的情况下计算的，从而导致一些（微小的）不准确。

SPSS Mann-Whitney U 检验 - 结论

正如我们刚才看到的，SPSS Mann-Whitney 检验输出可能包括多达 3 个不同的双侧 p 值。幸运的是，如果我们遵循 p < 0.05 时拒绝零假设的惯例，它们都会得出相同的结论：女性对“家庭用车”广告的评价高于男性 (p = 0.001)。其他两个广告没有显示出性别差异 (p > 0.10)。p 值为 0.001 表示概率为千分之一：如果男性和女性的_总体_对这个广告的评价相似，那么我们有千分之一的机会发现我们在_样本_中观察到的巨大差异。据推测，男性和女性的总体毕竟不会以相似的方式评价它。